
Kombinasyon Konu Anlatımı ve İçeriği
Kombinasyon, belirli bir kümeden belirli sayıda eleman seçme işlemini ifade eden bir matematiksel kavramdır. Sıralamanın önemsiz olduğu durumlarda kullanılır ve çeşitli alanlarda önemli bir yere sahiptir. Kombinasyon hesaplama yöntemleri ve günlük hayattaki uygulamalarıyla geniş bir kullanım alanına sahiptir.
Kombinasyon Konu Anlatımı Kombinasyon, belirli bir kümeden belirli sayıda eleman seçme işlemini ifade eden bir matematiksel kavramdır. Kombinasyon, sıralamanın önemli olmadığı durumlarda kullanılır. Bu bağlamda, kombinasyonun formülü, belirli bir kümeden r eleman seçimi için aşağıdaki gibi ifade edilir:
Burada;- n: Kümenin toplam eleman sayısı,- r: Seçilen eleman sayısı,- !: Faktöriyel sembolüdür. Kombinasyonun Önemi Kombinasyon, çeşitli alanlarda önemli bir yer tutar. Özellikle istatistik, olasılık teorisi, oyun teorisi ve karar verme süreçlerinde sıklıkla kullanılır. Kombinasyonların belirlenmesi, bir olayın olasılığını hesaplamak ve farklı alternatiflerin değerlendirilmesi açısından kritik bir öneme sahiptir. Kombinasyon ve Permütasyon Arasındaki Fark Kombinasyon ile permütasyon arasındaki temel fark, sıralamanın önemidir. Kombinasyon, elemanların sırasını dikkate almazken, permütasyon sıralamanın önemli olduğu durumları ifade eder. Örneğin, A, B ve C harflerinden 2 harf seçilecekse, kombinasyon ile AB ve BA aynı kabul edilirken, permütasyon için farklı sıralamalar olarak değerlendirilir.
Kombinasyon Hesaplama Yöntemleri Kombinasyon hesaplamak için birkaç yöntem bulunmaktadır. İlk olarak, doğrudan formül kullanımı yaygındır. Bunun yanı sıra, kombinasyonları hesaplamak için Pascal Üçgeni gibi yapılar da kullanılabilir. Pascal Üçgeni, her bir sayının üstündeki iki sayının toplamı ile oluşturulan bir üçgendir ve kombinasyon değerlerini kolayca bulmamıza yardımcı olur. Örnek Uygulamalar Örnek 1: 5 kişilik bir gruptan 3 kişiyi seçmek istiyoruz. Bu durumda kombinasyon hesaplaması şu şekildedir: C(5, 3) = 5! / (3! (5 - 3)!) = 10Yani, 5 kişilik gruptan 3 kişi seçmenin 10 farklı yolu vardır. Örnek 2: 10 farklı kitap arasından 4 kitap seçmek için: C(10, 4) = 10! / (4! (10 - 4)!) = 210Bu durumda, 10 kitap arasından 4 kitap seçmenin 210 farklı yolu bulunmaktadır. Kombinasyonun Günlük Hayattaki Uygulamaları Kombinasyon kavramı, günlük hayatta birçok alanda karşımıza çıkar. Örneğin;
Bu durumlar, kombinasyon kavramının ne kadar geniş bir uygulama alanına sahip olduğunu göstermektedir. Sonuç Kombinasyon, matematiksel bir kavram olarak, belirli bir kümeden eleman seçme işlemlerinde önemli bir rol oynamaktadır. Sıralamanın dikkate alınmadığı bu durum, çeşitli alanlarda uygulama bulmakta ve günlük hayatta karşılaştığımız birçok durumda hesaplamalar yapmamıza olanak tanımaktadır. Kombinasyon konusunda yapılan çalışmalar, matematiksel düşünme becerilerini geliştirmekte ve problem çözme yeteneğini artırmaktadır. |
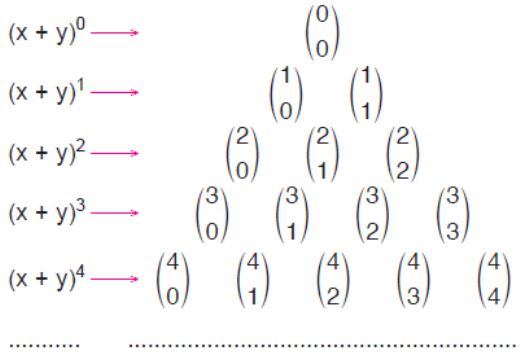















































Kombinasyon konusunda bazen kafam karışıyor. Örneğin, 5 elemanlı bir kümenin 3 elemanlı kombinasyonlarını hesaplarken neden 5! / [(5 - 3)! 3!] formülünü kullanıyoruz? Bu formülün mantığını biraz daha açıklar mısınız? Ayrıca, kombinasyon ve permütasyon arasındaki farkı anladım ama günlük hayatta hangi durumlarda kombinasyonu, hangi durumlarda permütasyonu kullanmam gerektiği konusunda örnekler verebilir misiniz?
Sevgili Ülmen,
Kombinasyon Formülü Mantığı:
5 elemanlı bir kümenin 3 elemanlı kombinasyonlarını hesaplarken kullandığımız formül olan 5! / [(5 - 3)! 3!] şu şekilde çalışır: Öncelikle, 5! (yani 5 faktöriyel) tüm elemanların sıralı permütasyonlarını verir. Ancak, biz sadece 3 elemanlı ve sırasız grupları istiyoruz. Bu yüzden, 5 - 3 = 2 elemanı dışarıda bırakmanın yollarını (2!) ve seçtiğimiz 3 elemanın kendi aralarındaki sıralı permütasyonlarını (3!) formülden çıkararak sadece sırasız kombinasyonları elde ederiz.
Kombinasyon ve Permütasyon Arasındaki Fark:
- Kombinasyon: Sıra önemli değilse kullanılır. Örneğin, bir salata yaparken hangi 3 sebzeyi seçeceğinizi belirlemek kombinasyon kullanmak demektir. Sıralama önem taşımaz.
- Permütasyon: Sıra önemliyse kullanılır. Örneğin, bir yarışmada 1., 2. ve 3. olan kişileri belirlemek permütasyon kullanmaktır, çünkü sıralama önemlidir.
Günlük Hayattan Örnekler:
- Kombinasyon: Bir kitap kulübünde 5 kitap arasından 3’ünü seçmek.
- Permütasyon: Bir sinema salonunda 3 kişilik bir koltuk diziliminde kimlerin hangi sırada oturacağını belirlemek.
Umarım bu açıklamalar kafandaki karışıklığı gidermene yardımcı olur, Ülmen. Başka soruların olursa çekinmeden sorabilirsin!