Matematik Mantık Konu Anlatımı Önermeler ve Doğruluk Değerleri Mantık, doğru ya da yanlış kesin hüküm bildiren önermelerden oluşur. Önermeler genellikle p, q, r gibi harflerle gösterilir. Bir önerme doğru ise p=1, Önerme yanlış ise p=0 şeklinde gösterilir. Genelde emir, istek, soru, ünlem bildiren ifadeler önerme değildir.
İki önerme için 4, üç önerme için 8 değişik durum vardır. O halde n tane önerme için 2 üzeri n şeklinde bulunabilir. Eşdeğer Önerme Doğruluk değerleri aynı olan önermelerdir. p ≡ q şeklinde gösterilir. P: "Ankara Türkiye'nin başkentidir." Q: "30+8=38" P=1 ve q=1 olduğundan p ≡ q olur. Önermenin Değili Bir önermenin olumsuzu alınarak elde edilen önermeye o önermenin değili denir. (') ifadesi ile gösterilir. P: 0 çift sayıdır. P=1 P': 0 çift sayı değildir. P'=0 Bileşik Önermeler İki ya da daha çok önermenin birbirine "veya", "ve", "ya da", "ise", "ancak ve ancak" bağlaçları ile bağlanması sonucunda elde edilen önermelerdir. P: Asal sayılar tek sayıdır. Q: İki tek sayının toplamı çift sayıdır. Önermeleri için; P veya q, pvq: "Asal sayılar tek sayıdır veya iki tek sayının toplamı çift sayıdır." önermesi bileşik önermedir. Veya Bağlacı P ile q önermeleri için; en az biri doğru iken doğru, ikisi de yanlış iken yanlış olan bileşik önermeye p veya q bileşik önermesi denir. Pvq ile gösterilir. ("v" veya bağlacı işareti) Ve Bağlacı P ve q önermeleri için ikisi de doğru iken doğru, geri kalan durumlarda yanlış olan önermeye p^q önermesi denir. ("^" ve bağlacı işareti) Ya Da Bağlacı P ile q önermeleri için bileşik önerme bileşenlerden sadece biri doğru iken doğru, diğer durumlarda yanlıştır. İse Bağlacı P => q şeklinde gösterilir. P doğru q yanlış iken yanlış, öteki bütün durumlarda doğrudur. Ancak ve Ancak Bağlacı P <=> q şeklinde gösterilir, p ile q'nun doğruluk değeri aynı iken doğru, farklı iken yanlıştır. Ekstra Bilgiler ve Uygulamalar Matematiksel mantık, bilgisayar bilimlerinde ve yapay zeka alanında da geniş uygulama alanı bulur. Doğruluk tabloları ve mantık kapıları, dijital devre tasarımında yaygın olarak kullanılır. Ayrıca, mantık önermeleri ve bağlaçları, algoritma geliştirme ve problem çözme süreçlerinde önemli bir rol oynar. Doğruluk Tablosu Örneği Doğruluk tabloları, önermelerin farklı doğruluk değerlerinde nasıl sonuçlar verdiğini gösterir.
Doğruluk tablosu şu şekilde olur:
Bu tablo, çeşitli önermelerin ve bileşik önermelerin doğruluk değerlerini analiz etmemizi sağlar. Matematiksel mantık, hem teorik hem de uygulamalı yönleriyle geniş bir çalışma alanı sunar. Temel kavramları anlamak, daha karmaşık mantıksal yapıları ve algoritmaları anlamanın anahtarıdır. |
Karateğin
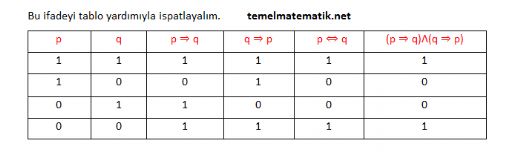
25 Temmuz 2024 PerşembeMantık konusunu anlamaya çalışıyorum ama p=>q bağlacının tam olarak ne zaman doğru ve ne zaman yanlış olduğunu karıştırıyorum. Özellikle, yağmur yağıyor ve şemsiye almadım örneğinde, p doğru ve q yanlış olunca neden p=>q yanlış oluyor?
Cevap yazAdmin
25 Temmuz 2024 PerşembeMerhaba Karateğin,
Mantık bağlaçları çoğu zaman kafa karıştırıcı olabilir, ancak temel kuralları anladığında daha kolay hale gelir. p => q (eğer p, o zaman q) bağlacının doğruluk tablosunu anlamak, bu konuda sana yardımcı olabilir. Bu bağlaca göre, p doğru ve q yanlış olduğu durumda, p => q ifadesi yanlış olur. Diğer tüm durumlarda ise bu bağlaç doğru kabul edilir.
Yağmur yağıyor ve şemsiye almadım örneğine gelirsek:
- p: Yağmur yağıyor (doğru)
- q: şemsiye almadım (yanlış)
Bu durumda, yağmur yağarken şemsiye almadığını söylersen (p doğru, q yanlış), bağlaç yanlış olur. Mantıkta p => q bağlacının yanlış olmasının sebebi, "Eğer yağmur yağıyorsa, o halde şemsiye almalısın" anlamına gelmesidir ve bu durumda şemsiye almadığın için p => q yanlış olur.
Umarım bu açıklama yardımcı olur. Mantığı anlamak zaman alabilir ama çalıştıkça daha kolay gelecektir.