
9 Sınıf Matematik Üçgenler Konu Anlatımı
Üçgenler, geometri alanında temel yapı taşlarıdır ve çeşitli türleri ile özellikleri sayesinde matematiksel problemlerin çözümünde önemli bir rol oynar. Bu yazıda, üçgenlerin tanımı, çeşitleri, alan hesaplama yöntemleri ve ilgili teoremler ele alınarak, geometri derslerinde öğrenilmesi gereken temel kavramlar üzerinde durulacaktır.
Üçgenler, geometri alanında önemli bir yere sahip olan temel şekillerdir. 9. sınıf matematik müfredatında üçgenlerin özellikleri, çeşitleri ve üçgenlerle ilgili teoremler detaylı bir şekilde işlenmektedir. Bu makalede, üçgenlerin tanımı, çeşitleri, alan hesaplama yöntemleri ve önemli teoremler üzerinde durulacaktır.Üçgen Nedir?Üçgen, üç kenarı ve üç açısı olan kapalı bir geometrik şekildir. Üçgenlerin kenar uzunlukları ve açıları, üçgenin özelliklerini belirler. Üçgenler, köşeleriyle birlikte üç noktadan oluşur ve bu noktalar, üçgenin köşeleri ya da dorukları olarak adlandırılır. Üçgen Çeşitleri Üçgenler, kenar uzunluklarına ve açı ölçülerine göre farklı kategorilere ayrılmaktadır. Bu çeşitler şunlardır:
Üçgenin Özellikleri Üçgenlerin bazı temel özellikleri vardır:
Üçgenin Alanı Üçgenin alanı, üçgenin taban uzunluğu ve yüksekliği kullanılarak hesaplanır. Alan formülü şu şekildedir:\[ \text{Alan} = \frac{1}{2} \times \text{Taban} \times \text{Yükseklik} \]Ayrıca, üçgenin kenar uzunlukları biliniyorsa, Heron formülü ile de alan hesaplanabilir:\[ s = \frac{a + b + c}{2} \]\[ \text{Alan} = \sqrt{s(s-a) (s-b) (s-c)} \]Burada \(a\), \(b\) ve \(c\) üçgenin kenar uzunluklarıdır ve \(s\) yarı çevredir. Üçgen Teoremleri Üçgenler ile ilgili bilinen bazı önemli teoremler şunlardır:
Sonuç Üçgenler, geometri ve matematikte temel bir yapı taşını oluşturmaktadır. 9. sınıf matematik dersinde üçgenlerin özellikleri, çeşitleri, alan hesaplama yöntemleri ve teoremleri üzerinde durulması, öğrencilerin matematiksel düşünme becerilerini geliştirmelerine yardımcı olmaktadır. Üçgenler, aynı zamanda mühendislik, mimarlık ve fizik gibi birçok alanda da önemli bir yere sahiptir. Ekstra Bilgiler |















































Bu içerikte üçgenler konusunun detaylı bir şekilde ele alındığı görülüyor. Özellikle üçgen çeşitlerinin kenarlarına ve açılarına göre sınıflandırılması, matematikte temel bir kavramdır. Üçgenin temel ve yardımcı elemanlarının tanımlanması da oldukça önemli, çünkü bu bilgiler ileride daha karmaşık geometri konularında yol gösterici olacaktır. Üçgenin iç açıları toplamının 180 derece olduğu bilgisi, birçok geometri probleminin çözümünde kritik bir rol oynar. Ayrıca, dış açıların toplamının 360 derece olduğu bilgisi, üçgenlerin özelliklerini daha iyi anlamamıza yardımcı olabilir. Ayrıca, yükseklik, kenarortay ve açıortay gibi yardımcı elemanların açıklanması, öğrencilerin üçgenler konusundaki kavrayışlarını pekiştirecektir. Bu kavramların geometrik şekiller ve çizimlerle desteklenmesi, öğrenmeyi daha da kolaylaştırabilir. Sonuç olarak, bu konuda verilen bilgiler, hem öğrenme sürecinde hem de daha ileri düzey matematikte sağlam bir temel oluşturmak için oldukça faydalı. Bu bilgilerin pratikte nasıl kullanılacağını öğrenmek, öğrencilerin üçgenler konusundaki becerilerini geliştirmelerine yardımcı olacaktır. Bu konuyla ilgili daha fazla örnek uygulama yapmak, pekiştirme açısından yararlı olabilir.
Üçgenler Konusunun Önemi
Amil, üçgenler konusunun detaylı bir şekilde ele alınması, matematiksel düşünmenin temel taşlarından birini oluşturuyor. Üçgen çeşitlerinin kenar ve açılara göre sınıflandırılması, öğrencilerin geometriye olan bakış açılarını genişletiyor ve temel kavramları pekiştiriyor.
Temel Elemanlar ve Açılar
Üçgenin iç açıları toplamının 180 derece olduğu bilgisi, birçok geometri probleminin çözümünde kritik bir rol oynuyor. Dış açıların toplamının 360 derece olduğunu bilmek ise üçgenlerin özelliklerini anlamayı kolaylaştırıyor. Bu tür bilgilerin pekiştirilmesi, öğrencilerin temel geometri bilgilerini sağlam bir şekilde edinmelerine yardımcı oluyor.
Yardımcı Elemanlar ve Geometrik Destek
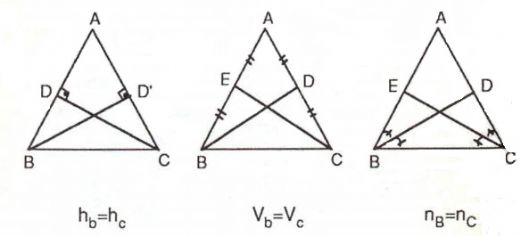
Yükseklik, kenarortay ve açıortay gibi yardımcı elemanların açıklanması, öğrencilerin üçgenlerle ilgili anlayışlarını derinleştiriyor. Bu kavramların geometrik şekiller ve çizimlerle desteklenmesi, öğrenmeyi daha etkili hale getiriyor. Görsel materyaller, soyut kavramların somutlaşmasına yardımcı olarak, öğrencilerin bilgiyi daha iyi içselleştirmelerini sağlıyor.
Pratik Uygulamalar ve Gelişim
Sonuç olarak, üçgenler konusundaki bilgiler, öğrencilerin matematiksel becerilerini geliştirmek için oldukça faydalı. Bu bilgilerin pratikte nasıl kullanılacağını öğrenmek, öğrencilerin kendilerine olan güvenlerini arttıracak ve daha ileri düzey matematik konularında daha sağlam bir temel oluşturmalarına yardımcı olacaktır. Bu konuyla ilgili daha fazla örnek uygulama yapmak, pekiştirme açısından son derece yararlı olabilir.