
Çember Konu Anlatımı ve İçeriği
Çember, geometri alanında temel bir kavramdır ve belirli bir merkez noktasından eşit uzaklıktaki noktaların oluşturduğu geometrik şekli ifade eder. Bu yazıda çemberin tanımı, elemanları, özellikleri ve çeşitli alanlardaki uygulamaları detaylı bir şekilde ele alınmaktadır.
Çember Konu Anlatımı ve İçeriği Çember, geometri alanında önemli bir yere sahip olan temel kavramlardan biridir. Çember, bir düzlemde belirli bir noktaya (merkez) eşit uzaklıkta bulunan noktaların kümesine verilen isimdir. Bu noktalar, çemberin çevresini oluşturur ve çemberin özellikleri, matematiksel hesaplamalar ve çeşitli uygulamalar açısından büyük önem taşır. Çemberin Tanımı Çember, düzlemdeki bir noktadan (merkez) belirli bir uzaklıkta bulunan tüm noktaların oluşturduğu geometrik şekildir. Matematiksel olarak, çemberin denklemi şu şekilde ifade edilir:- (x - a)² + (y - b)² = r²Burada (a, b) çemberin merkezi, r ise çemberin yarıçapıdır. Çemberin Elemanları Çemberin çeşitli elemanları bulunmaktadır:
Çemberin Özellikleri Çemberin bazı önemli özellikleri şunlardır:
Çemberin Uygulamaları Çemberin matematiksel özellikleri, mühendislik, fizik, mimari ve birçok diğer alanda geniş bir uygulama yelpazesine sahiptir. Örneğin:
Sonuç Çember, geometri ve matematikte temel bir kavram olarak karşımıza çıkmaktadır. Çemberin tanımı, elemanları, özellikleri ve uygulamaları, bu konunun derinlemesine anlaşılması açısından büyük önem taşır. Çember, hem teorik hem de pratik alanlarda önemli bir yer tutmakta ve birçok bilim dalında geniş bir uygulama alanına sahiptir. Ekstra Bilgiler Bu makale, çemberin tanımı ve özellikleri hakkında kapsamlı bir bakış açısı sunmakta ve çemberin matematik ve doğa bilimlerindeki önemini vurgulamaktadır. |
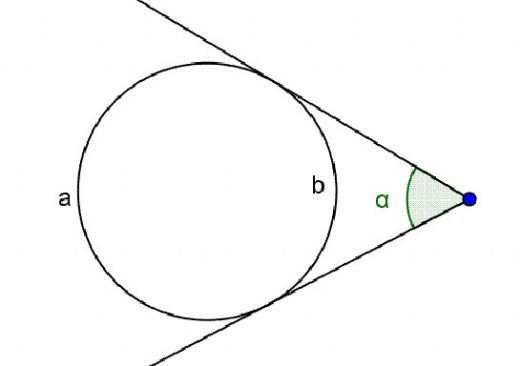















































Çemberin tanımını ve temel özelliklerini okuduğumda, çemberin ne kadar önemli bir geometri unsuru olduğunu bir kez daha anladım. Özellikle, merkez açının ve çevre açının tanımları arasındaki ilişki beni düşündürdü. Merkez açının yay ölçüsüne eşit olması, çevre açının ise yarısına eşit olması, bu iki açının ne kadar farklı ama birbiriyle bağlantılı olduğunu gösteriyor. Bu bilgiyi çember sorularında kullanmak, gerçekten de soruların çözümünü daha kolaylaştırıyor. Özellikle teğet kirişi açısının tanımını anlamak, çemberin teğetleri ile ilgili sorularda büyük bir avantaj sağlıyor. İç açı ve dış açı arasındaki farklar da oldukça ilginç; iç açının yayların toplamının yarısı olması, dış açının ise farklarının yarısı olması, geometri derslerinde dikkat edilmesi gereken noktalar. Kirişler dörtgeninin tanımı, çember içindeki açıların ilişkisini anlamak için çok faydalı. Bu bilgileri öğrenmek, çemberle ilgili problemleri çözmemde bana büyük bir yardımcı olacağını düşünüyorum. Sizce çemberin bu özelliklerini en iyi nasıl pekiştirebilirim?
Merhaba Sahabet,
Çemberin geometrik özelliklerini derinlemesine anlaman, matematiksel düşünme becerilerini geliştirmek açısından oldukça önemli. Çemberin merkez açısı ve çevre açısı arasındaki ilişkiyi kavraman, geometri sorularında büyük bir avantaj sağlıyor. Bu tür ilişkileri öğrenmek, özellikle çemberle ilgili problemleri daha kolay çözüme kavuşturmanı sağlıyor.
Özellikleri Geliştirme Yolları
Çemberin özelliklerini pekiştirmenin birkaç yolu var. Öncelikle, bu bilgileri sık sık pratiğe dökerek pekiştirebilirsin. Örneğin, çemberin çeşitli özelliklerini kullanarak problemler çözmek, öğrendiğin teorik bilgiyi uygulamaya dökmeni sağlar. Aynı zamanda, çember ile ilgili çeşitli sorular üzerinde çalışarak farklı senaryoları deneyimleyebilirsin.
Görsel Materyaller Kullanma
Görsel materyaller kullanarak çemberin özelliklerini anlamak da faydalı olabilir. Çizimler yaparak veya çeşitli geometri yazılımlarını kullanarak, açılar arasındaki ilişkileri görsel olarak incelemek, kavrayışını geliştirebilir.
Grupla Çalışma
Arkadaşlarınla birlikte çalışarak, çemberin özelliklerini tartışmak ve birbirinize sorular sormak da öğrenimini pekiştirebilir. Farklı bakış açıları, konuyu daha iyi anlamana yardımcı olacaktır.
Bu yöntemleri deneyerek, çemberin özelliklerini daha iyi pekiştirebilir ve geometri derslerinde başarılı olabilirsin. Başarılar dilerim!