Katı cisimler denildiğinde aklımıza küp, prizma ya da silindirler gelmelidir. Katı cisimler konu anlatımı, bu üç boyutlu geometrik şekillerin alan ve hacim hesaplamalarını içermektedir. Katı cisimler aşağıdaki konuları kapsamaktadır:
Katı cisimler konusu oldukça geniş bir bilgi ağına sahiptir ve matematikte önemli bir yer tutar. Piramitler Piramitler, bir tepe noktası olan ayrık üçgenlerin bir düzlem üzerinde birleşmesiyle oluşur. Bu üçgenlerin birleşmesini sağlayan taban şekli nasılsa o isimle adlandırılır. Örneğin, bu taban kare ise kare piramit, üçgen ise üçgen piramit olarak adlandırılır. Ayrıca, taban beşgen ya da altıgenden de oluşabilir. Katı cisimler konusu içinde en önemli başlıklardan biri katı cisimlerin hacimleridir. Üç boyutlu olmalarından dolayı hacimleri önem taşır. Piramitlerin hacimleri şu şekilde hesaplanır: Tepe noktasından tabanına bir 90 derecelik doğru çizilir ve bu yükseklik belirlenir. Taban alanı hesaplanır. Bu taban kare ise kare alanı, beşgen ise beşgenin alanı hesaplanır. Daha sonra 1/3 x taban alanı x yükseklik formülü kullanılır. Prizmalar Prizmalar, piramitlerden farklı olarak yan ayrıtları da taban gibi kare veya dikdörtgen olabilir. Yan ayrıtları kare olan prizmaya küp denirken, dikdörtgen olanına ise dikdörtgen prizma denir. Prizmalar taban şekline göre isimlendirilir. Ayrıca tabanı daire olan prizmalar silindir olarak adlandırılır. Prizmalarda da piramitler gibi tepe noktasından tabana bir dik çizilir ve yüksekliği bulunur. Bu yükseklik ile taban alanının çarpımı ile hacim bulunur. Koniler Koniler, tabanı daire olan ve bir üçgenin sarılmasıyla oluşan cisimlerdir. Katı cisimler konusu içinde koniler geniş bir yere sahiptir çünkü sıkça soru olarak karşımıza çıkmaktadır. Konilerin hacim hesaplaması, 1/3 x taban alanı x yükseklik formülü ile yapılır. Burada taban daire olduğu için dairenin alanını hesaplamanız gerekmektedir: πr² (pi çarpı yarıçapın karesi). Küreler Küreler, içi boş ve her yönden kapalı daireler olarak düşünülebilir. Kürenin merkezinden geçen doğru, kürenin çapını oluşturur. Kürenin yarıçapına r dersek, hacim formülü 4/3 x π x r³ (dört bölü üç pi çarpı yarıçapın küpü) olarak hesaplanır. Kürelerin yüzey alanı ise 4πr² (dört pi çarpı yarıçapın karesi) formülü ile bulunur. Ek Bilgiler Katı cisimlerin yüzey alanları ve hacimleri, mühendislik, mimarlık ve çeşitli bilim dallarında önemli uygulamalara sahiptir. Bu nedenle, doğru hesaplamalar yapmak büyük önem taşır. Ayrıca, bu konuların anlaşılması, ileri matematik ve fizik derslerinde de temel oluşturur. |
Özdel
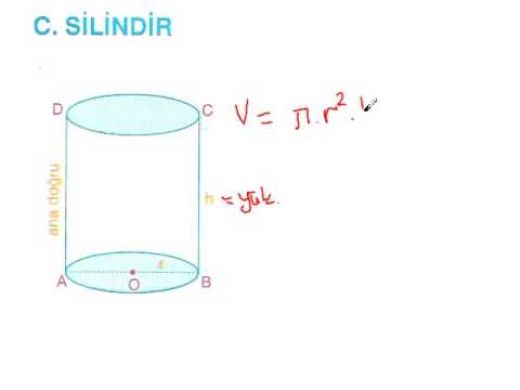
21 Temmuz 2024 PazarKatı cisimler dersi nasıl bu kadar geniş ve karmaşık olabilir? Hacim hesaplamalarında taban alanı ve yükseklik kullanılırken neden farklı formüller gerekiyor? Özellikle piramitlerde taban şekline göre adlandırma ve 1/3 ile çarpma neden gerekli? Kürelerin hacim ve yüzey alanı hesaplamalarında pi sayısının bu kadar önemli olmasını nasıl açıklayabiliriz?
Cevap yazAdmin
21 Temmuz 2024 PazarMerhaba Özdel,
Katı cisimler dersinin geniş ve karmaşık olması, geometrik şekillerin çeşitliliğinden ve her bir şeklin farklı özelliklere sahip olmasından kaynaklanıyor. Hacim hesaplamalarında taban alanı ve yükseklik kullanılması evrensel bir prensip olsada, şeklin özelliklerine göre farklı formüller geliştirilmiştir. Örneğin, piramitlerde taban şekline göre adlandırma ve hacmi hesaplarken 1/3 ile çarpma gerekliliği, piramitlerin geometrik yapısından kaynaklanır. Taban alanı ve yükseklik ile hacim hesaplanırken, piramitlerin yapısal olarak 1/3 oranında daha az hacim kapladığı göz önüne alınır.
Kürelerin hacim ve yüzey alanı hesaplamalarında pi sayısının önemine gelince, bu tamamen kürenin dairesel yapısından kaynaklanır. Pi sayısı, herhangi bir dairenin çevresi ile çapı arasındaki sabit oranı temsil eder ve kürelerin hesaplamalarında doğrudan kullanılır. Bu nedenle, pi sayısı kürelerin geometrik hesaplamalarında önemli bir rol oynar.
Umarım bu açıklamalar sorularına yanıt olabilmiştir.
Sevgiler,
Özdel